(Magneto-)Hydrodynamics
One-Dimensional
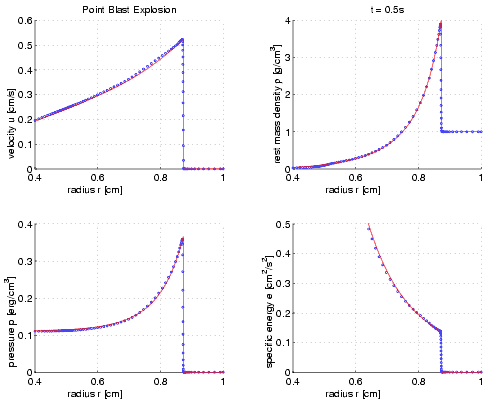
In spherical symmetry, the equations of hydrodynamics can be solved in full general relativity. This is done by our code AGILE. AGILE (Adaptive Grid Implicit Leap Extrapolation) is in principle a Newton-Raphson solver for roughly band-diagonal matrices which evolves a vector of unknowns in time using implicit finite differencing [Liebendoerfer, Rosswog & Thielemann 2002, ApJS, 141, 229]. AGILE features a dynamically adaptive grid which adjusts its resolution to gradients in the solution vector [Dorfi & Drury 1987, J. Comp. Phys., 69, 175]. The 'Leap Extrapolation' stands for a semi-implicit high-order time integration [Bader & Deuflhard 1983, Num. Math., 41, 373], which was advantageous in some test cases, but has not yet been implemented in astrophysical applications. The main technical advantage of AGILE is its automatic numerical construction of the Jacobi matrix, which reduces programming errors and facilitates the modification of the equations. The main technical disadvantage is that it is still an implicit scheme; any error or inconsistency in the equations is likely to result in convergence difficulties, which can make it a challenge to pinpoint the problem. The somewhat entangled mappings of the abstract solution vector used in the linear algebra procedures to specific zone and equation numbers in the physical description also do not facilitate debugging, even if numerical and physical procedures are properly separated throughout the code.
Agile has been used in models for X-ray bursts on accreting neutron stars [Felix Rembges 1999, Ph. D. thesis, University of Basel; Fisker et al. 2003, Nucl. Phys. A, 718, 614]. A version with general relativistic hydrodynamics in polar slicing and radial gauge has been used in the study of the effect of dark matter on the formation of supermassive black holes in the early universe [H. Mueller 2000, Diploma thesis, Landessternwarte Heidelberg]. Newtonian and general relativistic versions of AGILE provided the hydrodynamics for spherically symmetric supernova models with Boltzmann neutrino transport.
Three-Dimensional
Smoothed Particle Hydrodynamics (SPH)
Whitehouse & Bate 2006, MNRAS, 367, 32
Grid-Based Eulerian Magneto-Hydrodynamics
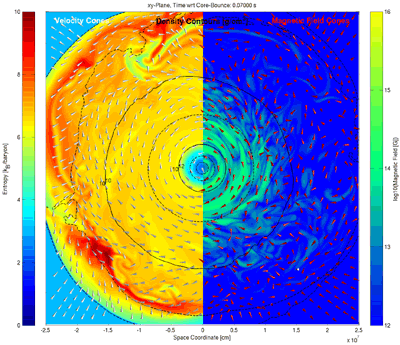
We parallelized the three-dimensional MHD code developed by [Pen, Arras & Wong 2003, ApJS, 149, 447] with MPI in cubic domain decomposition for distributed memory machines: at the time the MacKenzie cluster at CITA (Canadian Institute for Theoretical Astrophysics) and later our new project cluster SWIRL at the University of Basel. It was an important goal of this project to develop efficient codes for mid-size clusters (#Processors times #Cores/Processor ~ 100). For standard calculations we used 600 zones cubed in order to resolve the innermost region of stellar core collapse and postbounce evolution with equidistant zone widths of 1 km. Later and the current code versions are including a port to GPUs using OpenACC.
The picture on the left hand side shows an equatorial cut through a 3D simulation at 70 ms after bounce. This is 70 ms after a collapsed and compactified stellar core has bounced back at almost incompressible nuclear densities. A shock front emerges which stops its rapid expansion at a radius of a few 100 kilometers due to internal dissociation and neutrino losses. One black density contour line is labelled 10^12 g/cm^3. It approximately demarcates the rotating protoneutron star formed at the center of the simulation. The background color on the left hand side of the plot shows the matter entropy. Matter inside the stalled accretion shock is shock-heated and subject to fluid instabilities. Cool matter continues to accrete from the outside. The background color on the right hand side shows the magentic field strength. The field is wound up around the surface of the differentially rotating protoneutron star, further out it is entangled by the fluid instabilities. At this early stage, the field in this simulation is too weak to generate a strong dynamical impact. Movies of preliminary simulations are displayed here.
