Toward three-dimensional simulations of stellar core collapse with magnetic fields
The following very brief overview has been adapted from M. Liebendörfer, S. Whitehouse, & T. Fischer (2006), in Proceedings of IAU Symposium no. 239, "Convection in Astrophysics", Eds. F. Kupka, I. W. Roxburgh & K. L. Chan.
Stellar core collapse
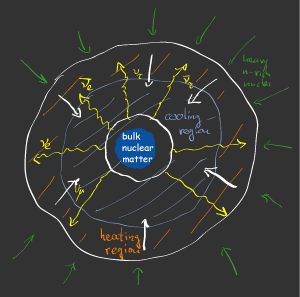
Nuclear fusion at the center of a gravitationally bound star drives the composition toward elements which accomodate the maximum binding energy per baryon. Gravitational compression no longer releases new fusion energy. Instead, the compression of the electron gas pushes the electrons into high energy levels from where they are captured by protons. Compressional heating is limited by the endo-energetic photo-dissociation of nuclei. Due to reduced pressure support the inner core collapses to nuclear density within a fraction of a second. The small compressibility of nuclear matter halts the subsonic infall of the innermost 0.5 M by an elastic collective bounce whose kinetic energy is almost immediately depleted by the dissociation of heavy nuclei and the emission of neutrinos. This matter forms the cold core of the newborn protoneutron star (PNS).
The sound speed in the outer layers decreases with radius so that their collapse becomes delayed with respect to the inner core. Their supersonic infall is terminated by an accretion shock at the outskirts of the PNS where the conversion of the infall energy to heat dissociates the heavy nuclei. The accreted matter compactifies by the emission of neutrinos and slowly settles onto the PNS. Even if the net mass flux is always directed toward the center, the accretion shock will expand to a radius km by the puffed-up volume of the hot matter behind the shock. At about 100 ms after bounce, the rapidly decreasing accretion rate leads to a roughly stationary position of the accretion shock where the volume of freshly accreted matter is compensated by the compactification of neutrino-emitting matter at the surface of the PNS.
The puzzling supernova explosion mechanism
In order to produce the observed supernova explosions the gravitationally bound layers between the PNS and the accretion shock must aquire enough energy to rapidly expand and eject the outer layers of the progenitor star. An important way of energy exchange between the different regions is the emission and absorption of neutrinos by the reactions e- + p <-> n + ve and e+ + n <-> p + v--e . Most of the energy of gravitational collapse (few times 1053 erg) is radiated away from the surface of the PNS over a time scale of several seconds. The delayed supernova explosion mechanism (Bethe & Wilson (1985)) assumes that enough of the emitted neutrino energy is absorbed behind the stalled accretion shock to explain the observed kinetic explosion energies of order 1051 erg. The verification of this scenario has been attempted in one-, two-, and three-dimensional computer models.
1D: One-dimensional simulations are carried out in spherical symmetry. Not to dispute the observed asymmetries in supernova explosions, but to accurately evaluate the interplay of nuclear and weak interactions, detailed radiative transfer of neutrinos, and full general relativity. The steep energy dependence of the weak interactions and the disparate time scales necessitate computationally expensive implicit multi-frequency radiative transfer calculations. Converging results by independent groups solving Boltzmann's transport equation showed that the energy transfer by neutrinos is relevant for the dynamics, but not sufficient to drive a spherically symmetric explosion (Rampp & Janka (2000); Liebendörfer et al. (2001);Thompson, Burrows, & Pinto (2003); Sumiyoshi et al. (2005)). The neutrino luminosity originates to about equal parts from accretion and from the diffusive neutrino flux out of the PNS. If neutrino heating produces outflows, the accretion rate is reduced, and with it the driving neutrino luminosities. Spherically symmetric models suffer from this negative feedback.
2D: Neutrino heating is more efficient in axisymmetric supernova models where the negative entropy gradient behind the accretion shock induces large-scale convective turnover (Herant et al. (1994)). On the one hand, rising neutrino-heated streams can cool by expansion and therewith increase the ratio of absorbed to emitted neutrinos. On the other hand, accretion flows persist in narrow downstreams alongside uprising matter and continue to feed the neutrino luminosity during the onset of the explosion. Several groups work on the extension of neutrino transport techniques developed in 1D to axisymmetric simulations. Although first simulations are more optimistic than in 1D, explosions are still absent for traditional progenitor masses (Buras et al. (2003)), while explosions are obtained for low-mass progenitors where the density in outer layers drops abruptly (Kitaura, Janka & Hillebrandt 2006); Dessart et al. (2006)).
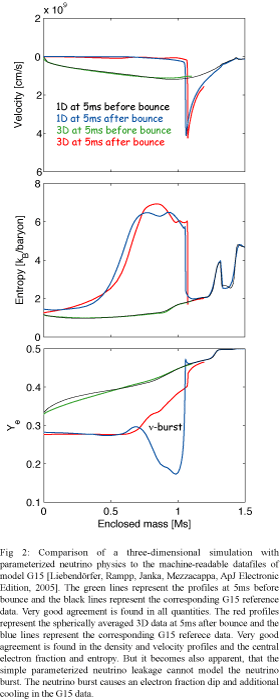
3D: The degrees of freedom in 3D are essentially richer: In 2D, a bubble is represented by a collectively moving torus, and a narrow downflow becomes a global accretion cone instead of a local funnel. In 2D, all oscillation modes are projected onto the symmetry axis. Three-dimensional simulations of stellar core collapse and postbounce phase have been carried out (Fryer & Warren (2004)), but with neutrino transport approximations that are difficult to compare to 1D results. Here, we parameterize the deleptonization in the collapse phase with a tabulation of the electron fraction as function of density in a reference simulation with Boltzmann neutrino transport. Estimates of entropy changes and neutrino stress are also deduced (Liebendörfer (2005)). The comparison of the 3D parameterized run with reference model G15 shows that the 1D results are accurately reproduced in the collapse phase. However, the accuracy breaks down with the launch of the neutrino burst. Better approximations are needed in the postbounce phase.
Fluid instabilities and magnetic fields in preliminary 3D models
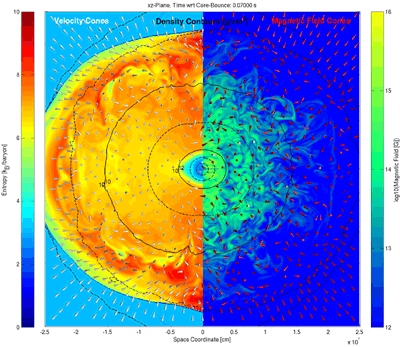
The collapse and bounce dynamics are evolved by a 3D MHD code (Pen, Arras, & Wong (2003);Liebendörfer, Pen, & Thompson (2006). A nuclear equation of state (Lattimer & Swesty (1991) is used and the spherically symmetric gravity includes general relativistic effects (Marek et al. (2006). Simulations are launched from the 15 M progenitor model of Woosley & Weaver (1995) with an initial magnetic field of 5 x 109 Gauss at a reference density of 5 x 107 g/cm3. The 3D computational domain consists of a central region of 600 km3, treated in Cartesian coordinates with a resolution of 1 km. The flow exterior to the 3D computational domain is evolved in spherical symmetry. As the duration of the collapse phase is no longer than a fraction of the imposed rotational period (1 s) the magnetic field does not wind up during collapse. Its amplification by about two orders of magnitude is due to the compression of field lines. A poloidal initial field produces at bounce a biconical shape, focussed on the protoneutron star. Toroidal initial fields tend to remain toroidal. After bounce, the declining strength of the shock results in a negative entropy gradient and asymmetries of the accretion shock develop in the equatorial plane. The magnetic field lines are entangled by convection and wind up around the PNS (movies).
Recent 2D investigations raised questions that are difficult to clarify if the fluid instabilities cannot unfold in 3D. For example, the occurence of the stationary accretion shock instability (Blondin, Mezzacappa, & DeMarino (2003)) needs to be investigated in 3D with reliable neutrino interactions. Or the question must be analyzed whether g-mode oscillations of the PNS are sufficiently excited by accretion flows to emit powerful sound waves (Burrows et al. (2006). Moreover, the influence of magnetic fields and rotation on the explosion mechanism are long-standing questions which have gained new momentum with the advent of axisymmetric simulations (Akiyama et al. (2003); Thompson, Quataert, & Burrows (2005); Ardeljan, Bisnovatyi-Kogan, & Moiseenko (2005); Fujimoto et al. (2006); Obergaulinger et al. (2006). Do MHD waves or reconnection contribute to the fragile neutrino heating; how relevant are analogies to solar MHD phenomena? It is the conspiration of three circumstances that make reliable 3D supernova models a challenge: (a) The rich and energy-dependent neutrino interaction and nuclear physics input. (b) The non-local 3D coupling of turbulent matter by radiative transfer on disparate characteristic time- and density-scales. (c) The explosion as a small surface effect with respect to the large reservoir of internal and gravitational binding energy enclosed in the PNS, necessitating thoughtful discretization and care about details.
